The hashing algorithm is one of the foundational components that ensure security and integrity within a blockchain network. In this comprehensive article, we will explore in detail how hashing works in blockchain, the essential properties of cryptographic hash functions, and why they are critical to decentralized systems. We will examine the SHA-256 algorithm step by step, discuss the structure and purpose of Merkle trees, and look at how Proof of Work leverages hashing to achieve consensus. Finally, we will cover practical examples, compare various blockchain projects’ approaches to hashing, and examine future directions such as post-quantum hash functions and advanced Merkle structures. This article is designed for readers ranging from enthusiasts new to the technology to engineers seeking deeper understanding, totaling over 2,000 words of detailed analysis.
1. What Is Hashing and Why Is It Needed
1.1 Fundamental Concepts
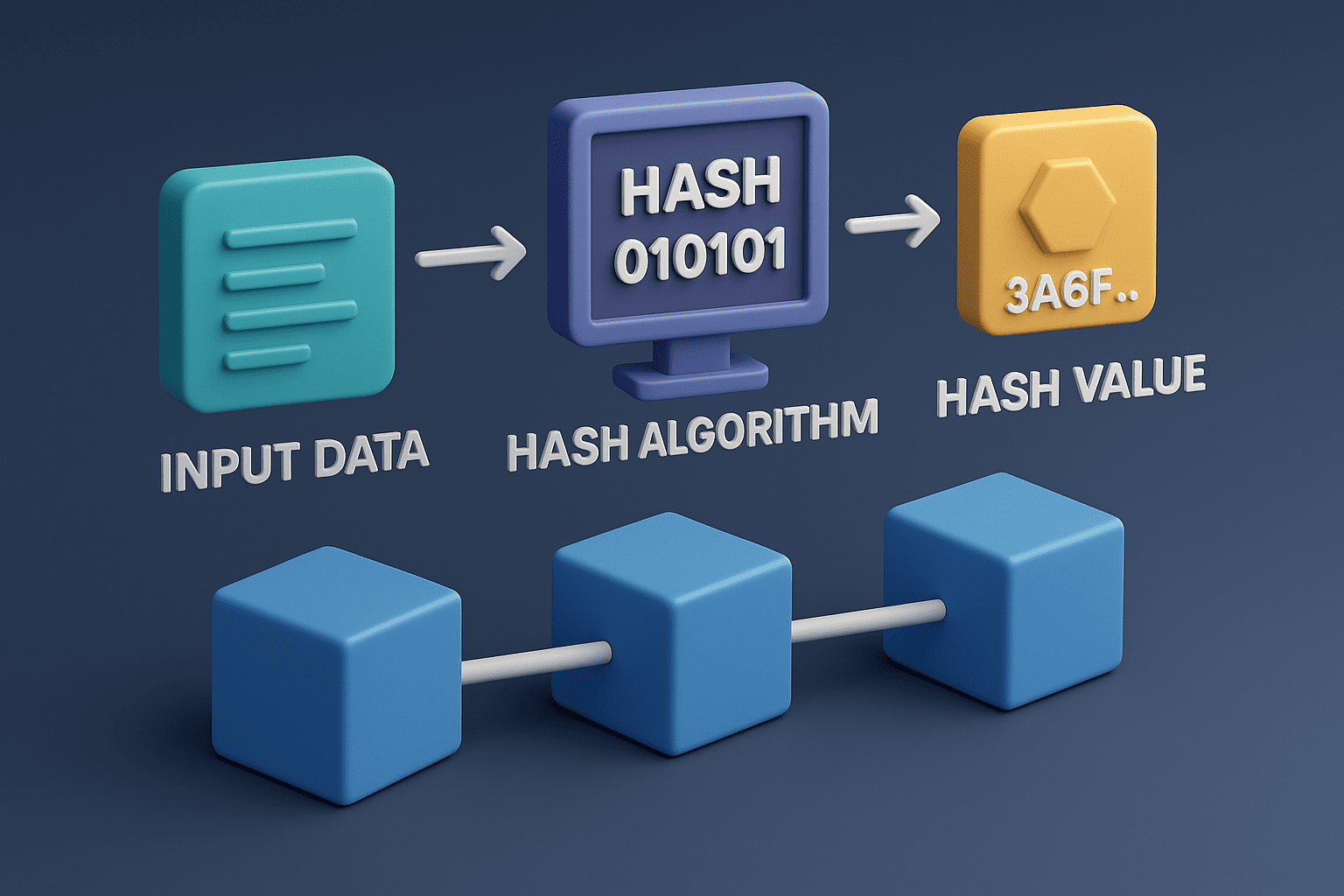
Hashing is the process of converting an arbitrary size input (such as a message or data block) into a fixed-size output string known as a hash or digest. The algorithm performing this transformation is referred to as a hash function. There are many different hash algorithms, but in the context of blockchain, cryptographic hash functions such as SHA-256, SHA-3, Scrypt, and others are most commonly used. These algorithms produce a unique, fixed-length output that represents the input data.
1.2 Properties of Cryptographic Hash Functions
For a hash function to be suitable in blockchain applications, it must exhibit several key properties:
- Determinism: The same input will always produce the same hash output. This consistency is crucial for verifying data integrity.
- Efficiency: Computing the hash for any input should be fast, regardless of the input size.
- Preimage Resistance (One-Way Property): Given an output hash, it should be computationally infeasible to reverse-engineer the original input.
- Avalanche Effect: A slight change in the input (even a single bit) should produce a drastically different hash output, preventing attackers from making predictable modifications.
- Collision Resistance: It should be extremely unlikely to find two distinct inputs that produce the same hash. This ensures that each dataset or transaction is uniquely represented.
These properties enable hash functions to be used for data verification, unique identifiers, and as the basis for complex consensus mechanisms like Proof of Work. Without these properties, blocks could be tampered with or manipulated without detection.
2. Role of Hashing in Blockchain
2.1 How Hash Functions Are Applied in Blocks
In a blockchain, each block contains a collection of data (transactions, metadata, a timestamp) and references the previous block via its hash. A typical block structure includes the following fields:
- Previous Block Hash: The hash of the previous block, which links blocks together in a chain.
- Transaction List: All transactions included in the block, serialized in a specific format.
- Timestamp: The time at which the block was created, usually represented in Unix time (seconds since January 1, 1970).
- Nonce: A number that miners adjust during the mining process to achieve a hash that meets the network’s difficulty requirement.
- Block Hash: The resulting hash calculated over all the above fields. This serves as the unique fingerprint of the block’s contents.
To create a valid block, miners repeatedly change the nonce and compute the hash of the block header until they find a hash that satisfies the target difficulty (e.g., begins with a certain number of leading zeros). This process, known as mining, demonstrates that significant computational work has been expended (Proof of Work) and that the block is valid within the current difficulty constraints.
2.2 Ensuring Data Integrity and Security
If any data within a block is altered—such as modifying a single transaction—the resulting hash of that block will change completely due to the avalanche effect. Because each block’s header includes the previous block’s hash, tampering with a single block breaks the chain for all subsequent blocks. In a decentralized network where every participant maintains a full copy of the blockchain, it becomes virtually impossible to alter historical data across the entire network faster than new blocks can be added. Thus, hashing provides a tamper-evident, immutable history of transactions.
3. The SHA-256 Algorithm: Standard in Cryptocurrencies
3.1 What Is SHA-256?
SHA-256 (Secure Hash Algorithm 256-bit) is part of the SHA-2 family of cryptographic hash functions developed by the National Institute of Standards and Technology (NIST). It produces a 256-bit (32-byte) hash value, typically rendered as a 64-character hexadecimal string. Its security is based on its resistance to collisions, one-wayness, and the avalanche effect, making it a popular choice for blockchain applications, particularly in Bitcoin.
3.2 Step-by-Step Overview of SHA-256
The following describes the major steps in computing a SHA-256 hash for a given message. While actual implementations involve bitwise operations and specific constants, this outline provides a conceptual framework:
- Padding (Message Augmentation):
- Append a single '1' bit to the end of the original message.
- Append enough '0' bits so that the total length (in bits) is congruent to 448 modulo 512.
- Append the original message length as a 64-bit big-endian integer.
- The result is divided into 512-bit message blocks for processing.
- Initialization: Eight 32-bit initial hash values (H0 through H7) are defined by standards. These constants are derived from the fractional parts of the square roots of the first eight prime numbers (2 through 19).
-
Processing Each 512-bit Block:
-
Message Schedule (W0 – W63):
- Divide the 512-bit block into sixteen 32-bit words W0 to W15.
- For i from 16 to 63, compute: Wi = σ1(Wi–2) + Wi–7 + σ0(Wi–15) + Wi–16, where σ0 and σ1 are defined bitwise functions (rotations, shifts, XOR).
-
Initialize Working Variables: Set A = H0, B = H1, C = H2, D = H3, E = H4, F = H5, G = H6, H = H7.
-
Main Compression Loop (64 Rounds): For i from 0 to 63:
- T1 = H + Σ1(E) + Ch(E, F, G) + Ki + Wi
- T2 = Σ0(A) + Maj(A, B, C)
- H = G; G = F; F = E; E = D + T1; D = C; C = B; B = A; A = T1 + T2
Where Σ0, Σ1, Ch, and Maj are bitwise functions defined by the SHA-256 standard, and Ki are 64 round constants derived from the fractional parts of the cube roots of the first 64 prime numbers.
-
Update Hash Values: After 64 rounds, compute: H0 = H0 + A; H1 = H1 + B; …; H7 = H7 + H.
-
- Final Hash Output: After processing all message blocks, concatenate H0 through H7 to produce the final 256-bit hash. Any single-bit change in the original message will result in a drastically different hash due to the avalanche effect.
This rigorous transformation ensures that SHA-256 is both collision-resistant and preimage-resistant for sufficiently long inputs, making it ideal for validating block headers.
3.3 Double SHA-256 in Bitcoin
Bitcoin applies SHA-256 twice (double SHA-256) to the block header. Specifically:
- First, compute H1 = SHA-256(block_header).
- Then compute H2 = SHA-256(H1).
The resulting H2 is compared against the current target threshold (difficulty target). Only if H2 is less than or equal to the target is the block considered valid. Double hashing was chosen to mitigate theoretical vulnerabilities and strengthen collision resistance. Any modification to the block header—such as changing a transaction—requires recalculating the hash twice, so adversaries cannot easily alter historical blocks without redoing all the work.
4. Merkle Tree Structure and Its Role
4.1 Fundamentals of Merkle Trees
A Merkle tree (or hash tree) is a binary tree in which each leaf node contains the hash of an individual transaction, and each non-leaf (internal) node contains the hash of the concatenation of its two child nodes’ hashes. The single hash at the top of the tree is known as the Merkle root and summarizes the entire set of transactions in that block. If any transaction changes, its leaf hash changes, propagating upward and altering the Merkle root, thus indicating tampering.
4.2 Constructing and Verifying a Merkle Tree
- Hash Individual Transactions: Compute the hash of each transaction using a chosen hash function (e.g., SHA-256). These become the leaf nodes.
- Pair and Hash Upward: For each pair of leaf hashes, concatenate them and compute the hash of that concatenation to form the parent node’s hash.
- Recurse Until Root: Continue pairing hashes at each level until a single hash remains at the top—this is the Merkle root.
- Handling Odd Number of Leaves: If there is an odd number of leaf nodes, duplicate the last hash to form a pair so that every level has an even number of nodes.
To prove that a given transaction is included in a block, a client only needs the transaction’s hash and the hashes of its “siblings” along the path to the root. This Merkle proof or Merkle path typically involves O(log n) hashes for n transactions. Lightweight clients (SPV nodes) can thus verify inclusion without downloading the entire block, greatly reducing bandwidth and storage requirements.
4.3 Advantages of Merkle Trees
- Space Efficiency: Only a small subset of hashes is needed to verify a single transaction, rather than the full transaction list.
- Fast Verification: Merkle proofs allow quick, O(log n) time checks of transaction inclusion.
- Scalability: As the number of transactions grows, the size of the proof grows logarithmically, making it practical even for large blocks.
5. Proof of Work: Why Hashing Complexity Matters
5.1 Proof of Work Mechanism
Proof of Work (PoW) is a consensus mechanism in which participants (miners) expend computational effort to solve a cryptographic puzzle—namely, finding a nonce that produces a block hash below a certain target threshold. In Bitcoin:
- Miners assemble a candidate block by including a list of transactions, a timestamp, the previous block’s hash, and an initial nonce.
- They compute the double SHA-256 hash of the block header. If the resulting hash is less than the network’s current target (based on difficulty), the block is valid and broadcast to the network.
- If the hash is not low enough, miners increment the nonce and hash again, repeating until a valid hash is found.
This iterative hashing demands immense computational resources and energy. It ensures that creating a new block requires real work, preventing Sybil attacks and making it computationally impractical for malicious actors to outpace the rest of the network.
5.2 Difficulty Adjustment
In Bitcoin, the difficulty target is recalibrated every 2,016 blocks (approximately two weeks) to maintain an average block generation time of 10 minutes. If blocks have been found faster than the target interval, difficulty increases; if slower, it decreases. This dynamic adjustment relies directly on hashing power in the network—more total hash rate leads to higher difficulty, and vice versa.
5.3 Cost of Attacks and Network Security
To successfully attack a PoW blockchain (e.g., execute a 51% attack), an adversary must control more than half of the network’s total hash rate. The required computational and energy costs for this exceed the potential benefits in most scenarios, making such attacks economically irrational. Thus, hashing functions underpin the security and immutability of PoW-based blockchains.
6. Examples of Hashing in Various Blockchain Projects
6.1 Ethereum and Keccak-256
Ethereum uses Keccak-256—a variant of the SHA-3 candidate—rather than SHA-256. Its uses include:
- Address Generation: Ethereum addresses are derived from the last 20 bytes of the Keccak-256 hash of a public key.
- Transaction Hashing: Every transaction’s data is hashed with Keccak-256 to produce a unique identifier.
- Ethash (Proof of Work): Ethereum’s PoW algorithm, Ethash, is designed to be memory-hard and ASIC-resistant by relying on Keccak-256 internally. Miners must access a large pseudorandom dataset called the DAG (Directed Acyclic Graph), preventing the dominance of ASIC hardware.
By choosing Keccak-256, Ethereum hardened itself against SHA-2–specific vulnerabilities and optimized its PoW for decentralization.
6.2 Litecoin and Scrypt
Litecoin opts for the Scrypt hashing algorithm instead of SHA-256 to reduce the advantage of specialized ASIC miners. Key attributes of Scrypt:
- Memory-Hardness: Scrypt requires significant memory (RAM) for computation, making it expensive to build ASICs that can outperform general-purpose hardware.
- GPU/CPU Friendliness: Ordinary GPUs and CPUs can mine Litecoin efficiently, promoting a more decentralized mining landscape.
- Adaptive Difficulty: Like Bitcoin, Litecoin adjusts its difficulty approximately every 2.5 minutes to target a 2.5-minute block time, with hashing power measured in Scrypt hashes per second.
6.3 Alternative Methods: Equihash and CryptoNight
Other blockchains use unique hashing approaches for specialized goals such as privacy or ASIC-resistance:
- Equihash: Used by Zcash, Equihash is a Proof of Work algorithm that is both memory- and CPU-intensive. It enables zk-SNARK (zero-knowledge) proofs for private transactions. Its memory hardness makes it resistant to ASICs, encouraging wider participation.
- CryptoNight: Employed by Monero, CryptoNight is designed to be ASIC-resistant by requiring frequent random memory accesses (ring buffers) and hashing over a large memory footprint. This enforces CPU/GPU mining and enhances user privacy by combining ring signatures and stealth addresses.
7. Practical Examples and Use Cases
7.1 Demonstrating SHA-256 Computation
Consider computing SHA-256 for a simple string “Hello, blockchain!”. Using any SHA-256 calculator, you would obtain approximately:
7509e5bda0c762d2bac7f90d758b5b2263a530d3adf1f7f3b6d5f5a9be1c9b7b
If you change just one character—e.g., “hello, blockchain!”—the hash completely changes due to the avalanche effect:
b8ae20f1b1ea8ec2d47f14f16a3dc61b7a8d89f5e8f8bb5f5e2f5e5bc2a0d8b9
This dramatic difference proves that even the slightest modification to the input yields a vastly different hash.
7.2 Building a Merkle Tree with Four Transactions
| Transaction | Transaction Hash (Leaf) |
|---|---|
| Tx1 | SHA-256("Tx1") = d1f7e6a1f89b4c8d23... (32 bytes) |
| Tx2 | SHA-256("Tx2") = e2a3d8f7c5b4a2d1f9... (32 bytes) |
| Tx3 | SHA-256("Tx3") = f3b5c7d9e8a4b6c2d5... (32 bytes) |
| Tx4 | SHA-256("Tx4") = a4c6d8e9f2b3c7a5d6... (32 bytes) |
Next, compute the intermediate nodes (level 1):
- Hash12 = SHA-256(d1f7e6a1f89b4c8d23... || e2a3d8f7c5b4a2d1f9...)
- Hash34 = SHA-256(f3b5c7d9e8a4b6c2d5... || a4c6d8e9f2b3c7a5d6...)
Then compute the Merkle root (level 2):
- MerkleRoot = SHA-256(Hash12 || Hash34)
This Merkle root is stored in the block header and reflects the combined integrity of all four transactions. To verify that Tx3 belongs in this block, a light client only needs the MerklePath: Tx3’s hash, its sibling leaf’s hash (Tx4), and the sibling of their parent (Hash12). Recomputing upward confirms the Merkle root without requiring all transaction data.
8. Advantages and Limitations of Hashing in Blockchain
8.1 Advantages
- Data Integrity: Hash functions immediately reveal any change to original data because even a single-bit modification yields a completely different hash.
- Security: Cryptographic properties make it computationally infeasible to reverse data or find collisions within a reasonable timeframe.
- Decentralized Verification: Each network participant can independently verify block integrity without trusting a third party.
- Efficient Transaction Proofs: Merkle proofs allow SPV clients to verify transaction inclusion rapidly using O(log n) data.
- Consensus Foundation: Proof of Work relies on hash computations to secure the network, making 51% attacks prohibitively expensive.
8.2 Limitations and Challenges
- High Energy Consumption (PoW): Mining requires extensive computational power and electricity to find a valid nonce, resulting in significant environmental impact.
- Scalability Concerns: Increasing transaction volume leads to larger block sizes and deeper Merkle trees, which can slow down verification and increase storage requirements.
- Implementation Complexity: Developing and optimizing secure hash functions across different platforms requires specialized cryptographic expertise.
- Quantum Vulnerabilities: Future quantum computers may be able to break existing hash functions like SHA-256 in a feasible time, necessitating a move to post-quantum algorithms.
9. Future Directions in Hashing Technology
Blockchain technology is rapidly evolving, and hashing remains central to new innovations. Key areas of development include:
9.1 Post-Quantum Hash Functions
As quantum computing advances, classical hash functions such as SHA-256 and SHA-3 could become vulnerable. Researchers are designing post-quantum cryptographic hash functions that rely on mathematical problems believed to be hard even for quantum computers (e.g., lattice-based constructions). These new hash functions aim to maintain collision resistance and one-way properties in a post-quantum era.
9.2 Optimizing Merkle Structures
High-throughput blockchains (IoT applications, large-scale networks) require more efficient Merkle trees to reduce storage and computational costs. Innovations include:
- Sparse Merkle Trees: Used for large but sparse data sets. Missing leaves are treated as default hashes, allowing compact representation and efficient proofs.
- Merkle Mountain Ranges: Employed in systems that produce multiple trees over time, enabling efficient appending of new data without recomputing entire structures.
9.3 New Consensus Mechanisms Involving Hashing
Beyond Proof of Work, various consensus algorithms continue to leverage hashing for different purposes:
- Proof of Stake (PoS): While it does not require heavy computational hashing, PoS uses hash functions for generating digital signatures and ensuring unpredictable validator selection.
- Proof of Authority (PoA): Relies on designated authorities to sign blocks. Hashing still underpins block validation and integrity.
- Proof of History (PoH): Used by Solana. PoH creates a cryptographic record of time by chaining hashes, producing a verifiable order of events without synchronized clocks.
10. Conclusion
The hashing algorithm is an indispensable component of blockchain technology, underpinning data integrity, security, and consensus. Through the properties of cryptographic hash functions—such as SHA-256—blockchains achieve tamper-evident records and robust protection against manipulation. Merkle trees enable efficient proof-of-inclusion mechanisms, while Proof of Work capitalizes on the computational difficulty of finding valid hashes to secure decentralized networks. Although challenges remain—such as high energy consumption, scalability hurdles, and looming quantum threats—ongoing research into post-quantum hash functions and optimized data structures promises to keep blockchain resilient and efficient. Understanding how hashing works is crucial to appreciating the foundations of blockchain systems and their continuing evolution.